| HOME | 地図投影法 | BACK | NEXT |
| 正性質 (2000/06/23) |
地図投影法は正しく表現できる性質によって分類することもできます。地図の性能ともいいます。主題を正しく表現するために必要な性質を備えた投影法を選択してください。
| ■ 地図のひずみ (distortion of a map projection) |
球を投影面に投影するわけですから、接していない部分では、ずれが生じることになります。これを「地図のひずみ」といいます。ひずみには種類があり、距離のひずみ、面積のひずみ、角度のひずみに分類することができます。光源の位置や補正の仕方を工夫することで、1つか2つのひずみを完全に除去することができます。1つも正しく表現できない投影法もありますが、それらは3つのひずみをバランスさせる、大圏コースを直線で表せる、緯線を水平で表せる、などの特徴を備えています。
| ■ 正距図法 (equidistant projection) |
正距とは、地球上の2地点間の距離が対応する地図の線上において、正しく比例して表現されることです。ただしすべての地点間ではありません(それができるのは地球儀だけです)。次の3つのうちの1つが正しい距離で表現できれば正距図法とみなされます。正しい長さで表現されている線を等長線とよびます。
a)ある特定の1点または2点から全ての地点への距離
b)全ての経線、あるいは全ての緯線の長さ(正軸法のとき)
c)接点を中心とした同心円の円弧の長さ
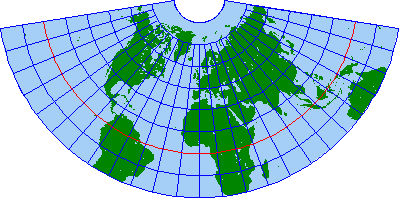
(図:ドリール正距円錐図法では全ての経線と標準緯線(ここでは北緯30度)の長さが正しい)

| ■ 正積図法 (equal-area projection) |
正積とは、地球上のどの部分についても、その面積比率が地図上に正しく表現されることです。分布図のような量的主題図に使われます。等積図法ともいいます。
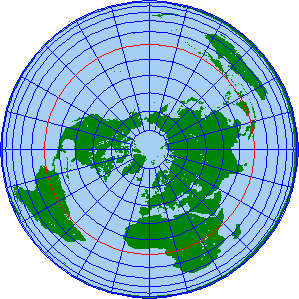
(図:ランベルト正積方位図法では緯線の間隔を補正して正積にしている)
| ■ 正角図法 (conformal projection / orthomorphic projection / isogonal projection) |
角が正しいとはどういうことでしょうか。これはかなり難解です。地球上の1地点において2つの方向線が作る角と、対応する地図上の2つの方向線が作る角が等しいと定義されています。任意の地点間の方向が正しく表現されるわけではありません。もう少しわかりやすく説明します。地球上に同じ大きさの小さな円がたくさんあると仮定した場合、正角図法で投影された地図上でも全ての円がほぼ真円で表されます。つまりごく狭い範囲に限れば形が正しいといえるため、「相似図法」ともよばれます。しかし円の大きさは緯度が高くなるにつれて拡大していくため、面積のひずみはかなり大きなものになります。
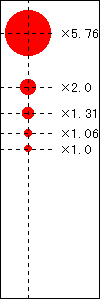
(図:メルカトル図法では、北緯80度は東西、南北ともに5.76倍に拡大される)